What is the center of a circle. How can you find the center of a circle using different methods. Why is the center of a circle important in geometry. What are the properties of a circle’s center.
Understanding the Center of a Circle: Definition and Importance
The center of a circle is a fundamental concept in geometry that plays a crucial role in defining and understanding circular shapes. But what exactly is the center of a circle, and why is it so important?
The center of a circle is defined as the fixed point from which all points on the circle’s circumference are equidistant. This point serves as the origin for all radii and diameters of the circle. Understanding the center is essential for various mathematical calculations and real-world applications involving circular objects.
Key Properties of the Center of a Circle
- It is equidistant from all points on the circumference
- All radii of the circle intersect at this point
- It is the midpoint of any diameter of the circle
- It is the point of symmetry for the entire circle
These properties make the center of a circle a critical reference point for various geometric calculations and constructions.
Four Methods to Find the Center of a Circle
Finding the center of a circle can be accomplished through several methods, each suited to different situations and available information. Here are four reliable techniques to locate the center of a circle:
1. Using Chords and Perpendicular Bisectors
This method involves drawing chords and their perpendicular bisectors to pinpoint the center. Here’s how it works:
- Draw two non-parallel chords on the circle
- Construct the perpendicular bisector of each chord
- The point where these bisectors intersect is the center of the circle
Why does this method work? The perpendicular bisector of a chord always passes through the center of the circle. By using two chords, we ensure a unique intersection point, which must be the center.
2. Using the Equation of the Circle
When given the equation of a circle, we can easily identify its center. The standard form of a circle’s equation is:
(x – h)² + (y – k)² = r²
In this equation, (h, k) represents the coordinates of the center, and r is the radius. By comparing the given equation to this standard form, we can directly read off the center’s coordinates.
3. Using the Endpoints of a Diameter
If we know the coordinates of two points that form a diameter of the circle, we can find the center using the midpoint formula:
Center (h, k) = ((x₁ + x₂)/2, (y₁ + y₂)/2)
Where (x₁, y₁) and (x₂, y₂) are the coordinates of the diameter’s endpoints.
4. Using Tangent Lines
This method utilizes the property that tangent lines are perpendicular to the radius at the point of tangency:
- Draw two tangent lines to the circle at different points
- Construct perpendicular lines from the points of tangency
- The intersection of these perpendicular lines is the center of the circle
The Significance of the Center in Circle Geometry
The center of a circle is not just a point of reference; it’s a crucial element in many geometric concepts and calculations. Understanding its significance can enhance our grasp of circular geometry and its applications.
Radii and Diameters
All radii of a circle are equal in length and originate from the center. This property is fundamental to the definition of a circle and is used in numerous calculations involving circular objects. The diameter, which passes through the center, is always twice the length of the radius.

Symmetry and Rotation
The center acts as a point of rotational symmetry for the circle. Any rotation of the circle around its center will result in a circle identical to the original. This property is crucial in many applications, from gear design to artistic compositions.
Inscribed and Circumscribed Shapes
The center plays a vital role in constructing shapes inscribed in or circumscribed around a circle. For example, regular polygons inscribed in a circle all have vertices equidistant from the center.
Practical Applications of Finding a Circle’s Center
The ability to locate and understand the center of a circle has numerous real-world applications across various fields. Let’s explore some practical uses of this geometric concept:
Engineering and Design
- Designing circular components in machinery
- Calculating the center of mass for circular objects
- Creating symmetrical patterns in architectural designs
Navigation and Mapping
- Determining the epicenter of seismic activity
- Calculating orbital paths of satellites
- Planning circular flight paths or shipping routes
Art and Graphics
- Creating balanced compositions in visual arts
- Designing logos and circular graphics
- Implementing circular user interface elements in software design
These applications highlight the importance of understanding and being able to locate the center of a circle in various professional and creative contexts.
Common Misconceptions About the Center of a Circle
Despite its fundamental nature, there are several misconceptions about the center of a circle that can lead to errors in understanding and application. Addressing these misconceptions is crucial for a comprehensive grasp of circular geometry.
Misconception 1: The Center is Always Visible
Many assume that the center of a circle is always a visible point on the circle itself. In reality, the center is often not part of the visible circle, especially in real-world objects like rings or circular tracks.
Misconception 2: All Points Inside a Circle Can Be Its Center
Some mistakenly believe that any point inside a circle could potentially be its center. However, there is only one unique point that satisfies the definition of being equidistant from all points on the circumference.
Misconception 3: The Center is Always at (0,0) in Coordinate Geometry
While it’s common to see examples where the center is at the origin (0,0), this is not always the case. The center can be at any point on the coordinate plane, and its position affects the equation of the circle.

Advanced Concepts Related to the Center of a Circle
As we delve deeper into circular geometry, several advanced concepts emerge that build upon our understanding of the circle’s center. These concepts are crucial in higher-level mathematics and have significant applications in various scientific fields.
Eccentric Circles and Eccentricity
Eccentric circles are circles that are not concentric (do not share the same center). The concept of eccentricity, which measures how much a conic section deviates from being perfectly circular, is closely related to the position of the center.
Circle Inversion
Circle inversion is a geometric transformation that uses the center of a circle as a key point. It involves “flipping” points from inside the circle to outside, and vice versa, based on their distance from the center.
Polar Coordinates and the Center
In polar coordinate systems, the center of a circle plays a crucial role. The equation of a circle in polar form changes based on whether the center is at the pole or at some other point.
Challenges in Finding the Center of Irregular or Incomplete Circles
While finding the center of a perfect circle is straightforward, real-world situations often present challenges when dealing with irregular or incomplete circular shapes. These scenarios require more advanced techniques and considerations.
Dealing with Ellipses and Near-Circular Shapes
In practice, many “circular” objects are actually slightly elliptical. Determining the center of these shapes requires understanding the concepts of major and minor axes and focal points.
Incomplete or Obscured Circles
When only a portion of a circle is visible or accessible, traditional methods may not be applicable. In these cases, statistical methods or best-fit algorithms might be necessary to estimate the center’s position.
Noisy Data in Digital Image Processing
When working with digital images, imperfections in the data can make it challenging to precisely locate the center of circular objects. Advanced image processing techniques, such as Hough transforms, are often employed in these situations.

Understanding these challenges and the methods to overcome them is crucial for professionals working in fields like computer vision, medical imaging, and astronomical data analysis.
The Role of the Center in Circle Theorems and Proofs
The center of a circle is a pivotal element in many important theorems and proofs in geometry. These theorems not only deepen our understanding of circular geometry but also provide powerful tools for solving complex geometric problems.
The Inscribed Angle Theorem
This theorem states that an angle inscribed in a circle is half the central angle subtending the same arc. The center of the circle is crucial in defining the central angle and proving this relationship.
The Perpendicular Chord Theorem
This theorem proves that the perpendicular line from the center of a circle to a chord bisects the chord. It’s a fundamental property that relies on the equidistance of the center from all points on the circumference.
Thales’ Theorem
Thales’ theorem states that any angle inscribed in a semicircle is a right angle. The center of the circle is essential in defining the semicircle and proving this property.
These theorems, among others, demonstrate the central role that the center plays in understanding and proving key geometric relationships within circles.
Center of Circle – Definition, Formula, Examples, Facts
What Is the Center of a Circle?
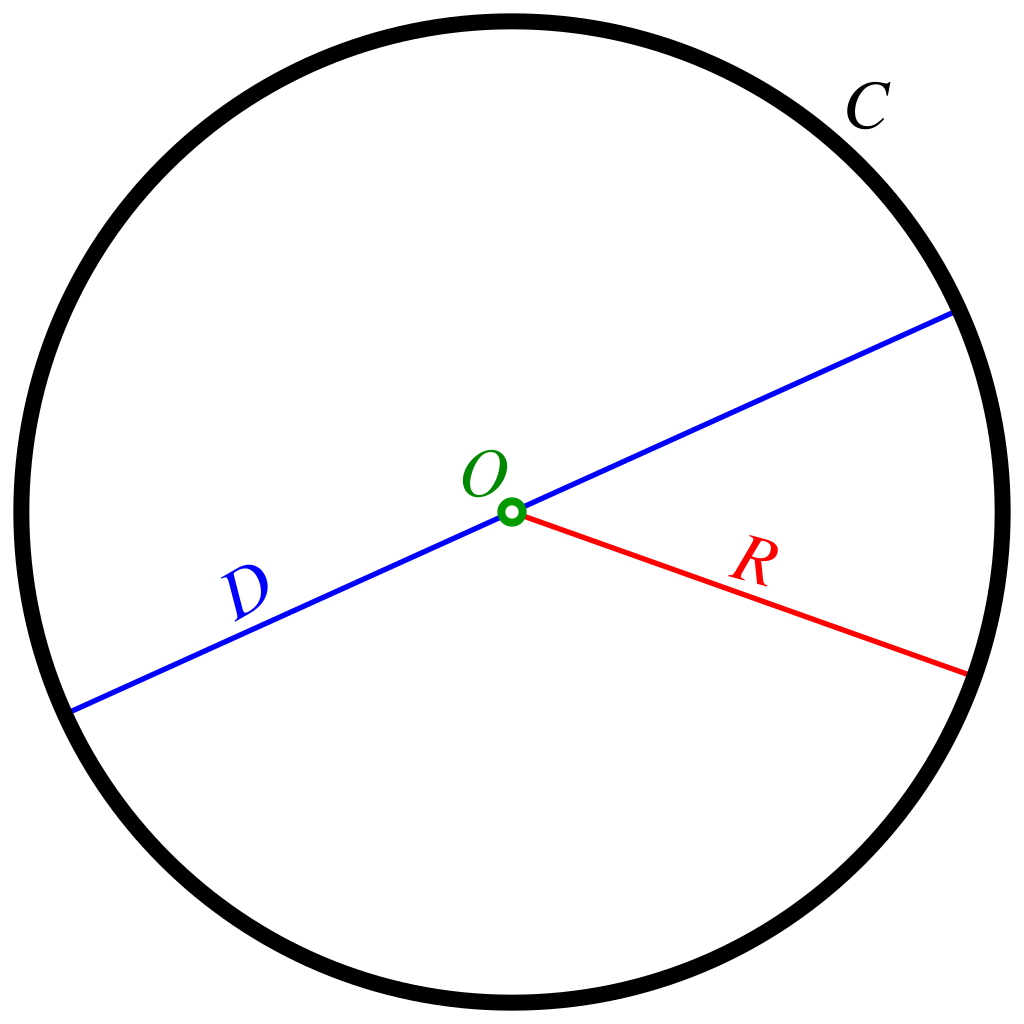
A circle is the set of all points (or locus of all points) in the plane that lie at a fixed distance from a fixed point. The fixed point is called the “center” of the circle. The fixed distance is called “radius.”
Center of a Circle: Definition
A circle is a two-dimensional shape defined by its center and radius. We can draw any circle if we know the center and radius. A circle can have an infinite number of radii. The center point is the midpoint where all radii intersect. It can also be defined as the midpoint of the diameter of the circle.
We can construct a circle of any radius using a compass. The distance between the pencil and the pointer of a compass is adjustable. Construct the center of a circle by keeping the pointer on any fixed point. Set the distance equal to the required radius. Draw a complete circle without changing this distance. The fixed point acts as the center of the circle. {2}$
{2}$
How to Find the Center of a Circle
To find the center of the circle, we’ll consider two cases:
- We need to locate the center of the given circle.
- We need to find the coordinates of the center of the circle using the equation of the circle.
When a circle is given
When we’re given a circle and we need to find its center, we can follow the steps listed below:
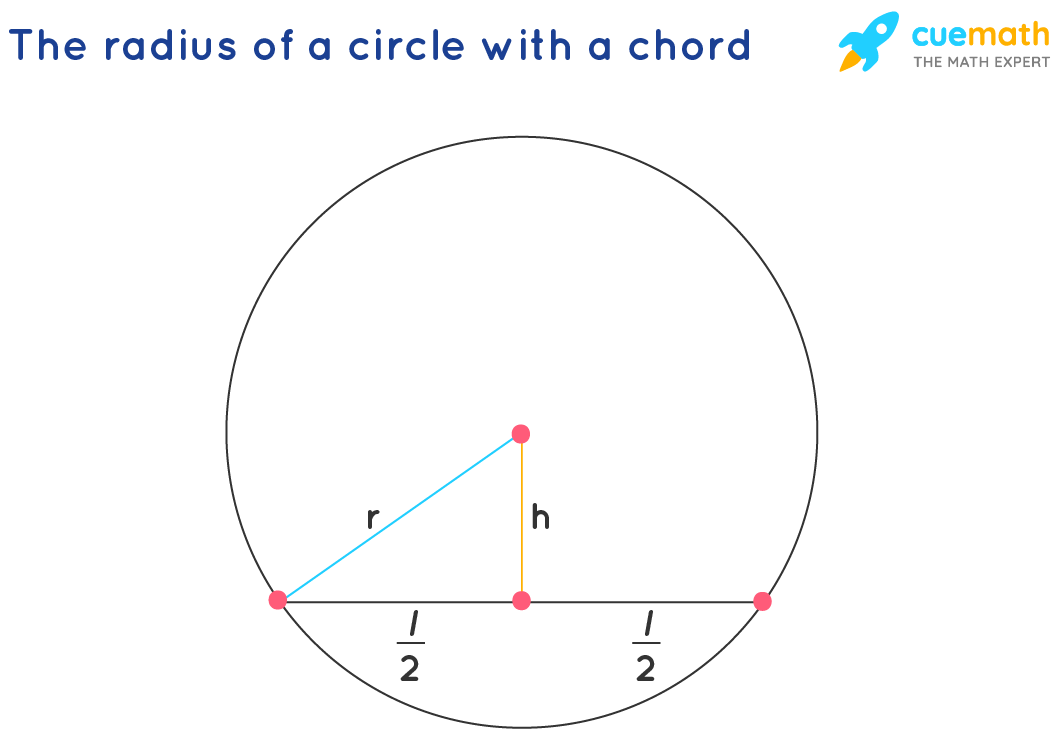
Step 1: Draw a chord AB in the circle and note down its length carefully .
Step 2: Draw another chord CD parallel to AB so that it is the same length as AB.
Step 3: Use a ruler to connect points P and N with a line segment.
Step 4: Connect points B and C.
Step 5: The intersection of AD and BC is the center of the circle.
In a similar way, the center of a circle can be found using secants (chords are the part of secant inside the circle). Also, we can use the perpendiculars of tangents at the point of contact to find the center. {2}\;-\;4y + 4$
{2}\;-\;4y + 4$
Comparing with the general equation we have h $= 0$, k $= 2$ and r $= 2$. Thus the center of the circle is (0, 2).
When endpoints of a diameter are given
If the endpoints of the diameter are given, then to find the coordinates of the center
point, we use the midpoint formula, since the center is the midpoint of the
diameter. The steps to find the center of the two points are as follows:
Step 1: Assume that the circle’s center is at these coordinates $(h,k)$.
Step 2: If $(h, k)$ is the midpoint coordinates of a line segment with
endpoints $(x_{1},\;y_{1})$and $(x_{2},\;y_{2})$, then by midpoint formula we can write
$(h, k) = (\frac{x_{1}+ x_{2}}{2},\frac{y_{1} + y_{2}}{2})$
Step 3: Simplify to get the coordinates of the center of the circle.
Let’s take an example of a circle where the endpoints of the diameters are $( \;-2,\;4)$ and $4(6, \;16)$.
Then, its center coordinates are:
$(h,k) = (\frac{-2+6}{2},\frac{4+16}{2})$
$(h,k)=(\frac{4}{2},\frac{20}{2})$
$(h,k)=(2,\;10)$
Therefore, the coordinates of the center of the circle whose endpoint is the diameter are (2,10).
Fun Facts about the Center of a Circle
- If a circle is divided into two equal parts, each part is called a semicircle. The diameter of a circle divides it into 2 semicircles.
- A sector of a circle is part of a circle in between two radii and an arc; there is a unique sector, formed by radii at right angles and is known as a quadrant.
- The perpendicular bisectors of any two chords of a circle always meet at the center of a circle.
Conclusion
The center of a circle is a point inside the circle, which is equidistant from all the points on the boundary of the circle. In this article, we learned about the center of a circle, its properties, and how to find the center of a given circle using different methods.
Solved Examples on Center of a Circle
1. Find the equation of a circle, given the coordinates of the center are (3, 1), and the radius of the circle is 5 units. Check if the origin lies inside the circle, on the circle, or outside of the circle. {2} = 12$ is the equation of a circle.
{2} = 12$ is the equation of a circle.
Expert Maths Tutoring in the UK
A circle is defined as the locus of a moving point on a plane such that its distance from a fixed point on the plane remains constant or fixed. That fixed point is called the center of the circle. Let us learn more about the center of a circle in this article.
| 1. | Center of Circle Definition |
| 2. | Center of Circle Formula |
| 3. | How to Find Center of Circle? |
| 4. | FAQs on Center of Circle |
Center of Circle Definition
A circle is a 2D shape defined by its center and radius. We can draw any circle if we know the center of circle and its radius. A circle can have an infinite number of radii. The center of a circle is the midpoint where all the radii meet. It can also be defined as the midpoint of the diameter of the circle. Observe the figure given below where O is the center of circle and OP is the radius.
It can also be defined as the midpoint of the diameter of the circle. Observe the figure given below where O is the center of circle and OP is the radius.
Center of Circle Formula
The center of circle formula is also known as the general equation of a circle. In a circle, if the coordinates of the center are (h,k), r is the radius, and (x,y) is any point on the circle, then the center of circle formula is given below:
(x – h)2 + (y – k)2 = r2
This is also known as the center of the circle equation. We will be using this formula in the following sections to find the center of a circle or the equation of the circle.
How to Find the Center of Circle?
In order to find the center of the circle, we will use some simple steps. There are two cases that might come up when we could be asked to find the center of a circle:
- When a circle is given and we need to find its center.

- When an equation of a circle is given and we need to find the coordinates of its center.
When a Circle is Given
When a circle is given to us and we need to find its center point, then we can follow the steps listed below:
Step 1: Draw a chord PQ in a circle and carefully note its length (which is 4 inches in the figure below).
Step 2: Draw another chord MN parallel to PQ such that it should be of the same length as PQ.
Step 3: Join the points P and N through a line segment using a ruler.
Step 4: Join points Q and M.
Step 5: The point of intersection of PN and QM is the center of the circle.
When Equation of the Circle is Given
If we know the equation of a circle, and we need to find its center, then we will use the following steps. Let us understand this with the help of an example.
Example: Let us find the coordinates of the center of a circle with equation x2 + y2 – 4x – 6y – 87 = 0
Solution: The steps to find the coordinates of the center of a circle are listed below:
- Step 1: Write the given equation in the form of the general equation of a circle: (x – h)2 + (y – k)2 = r2, by adding or subtracting numbers on both sides.
We can write the given equation as x2 – 4x + y2 – 6y = 87. Add 4 to both sides of the equation to get a perfect square of x-2. So, we will get, x2 – 4x + 4 + y2 – 6y = 87 + 4.
⇒ (x – 2)2 + y2 – 6y = 91
Add 9 to both sides to get a perfect square of y – 3
⇒ (x – 2)2 + y2 – 6y + 9 = 91 + 9
⇒ (x – 2)2 + (y – 3)2 = 100
⇒ (x – 2)2 + (y – 3)2 = 102
This looks like the general equation of circle.
- Step 2: Compare this equation with the general equation and identify the values of h, k, and r.
If we compare (x – 2)2 + (y – 3)2 = 102 with (x – h)2 + (y – k)2 = r2, we can identify that h = 2, k = 3, and r = 10. So, we have got the coordinates of the center of circle which are (h, k) = (2, 3).
How to Find the Center of Circle with Two Points?
If the endpoints of the diameter of the circle are given, then to find the coordinates of the center we use the mid-point formula, because the center is the mid-point of the diameter of the circle. The steps to find the center of a circle with two points are given below:
- Step 1: Assume that the coordinates of the center of the circle are (h, k).
- Step 2: Use the midpoint formula which says that if (h, k) are the coordinates of the midpoint of a segment with endpoints (x1, y1) and (x2, y2), then (h, k) = [(x1 + x2]/2, [y1 + y2]/2).

- Step 3: Simplify it and get the coordinates of the center of the circle.
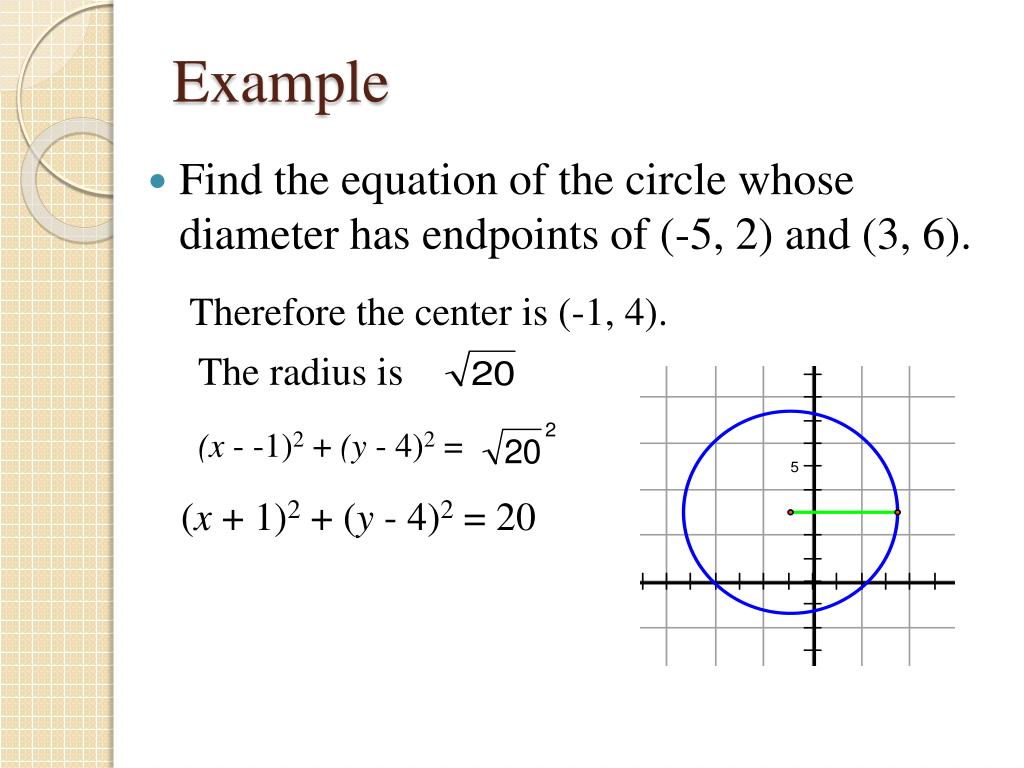
Let us take an example of a circle in which the endpoints of a diameter are given as (-2, 4), and (6, 16). Then, the coordinates of its center are:
(h, k) = [(-2 + 6)/2, (4 + 16)/2]
(h, k) = (4/2, 20/2)
(h, k) = (2, 10)
Therefore, the coordinates of the center of a circle with the endpoints of diameter are (2, 10).
☛ Related Articles
Check these interesting articles related to the concept of center of circle in geometry.
- Circle Formulas
- Sector of a Circle
- Circumference of Circle
- Area of Circle
FAQs on Center of Circle
What is the Center of Circle?
The center of a circle is the point where we place the tip of our compass while drawing a circle. It is the mid-point of the diameter of the circle. In a circle, the distance between the center to any point on the circumference is always the same which is called the radius of the circle.
What are the Coordinates for the Center of the Circle and the Length of the Radius?
The coordinates of the center of the circle represent the distance of the center point from the x-axis and y-axis respectively. It is generally denoted in the form of (h, k), where h and k represent the x and y coordinates respectively. The length of the radius is denoted by r. The coordinates of the center and the radius are related to each other in the form of an equation: (x – h)2 + (y – k)2 = r2.
What is the Center of a Circle Represented by the Equation (x – 5)
2 + (y + 6)2 = 42?
If we compare the given equation with the general equation of center of circle: (x – h)2 + (y – k)2 = r2, we can see that h = 5, k = -6, and r = √42. So, the center of the circle is at (5, -6).
How to Find Center of Circle?
To find the center of a circle, we can draw two parallel chords having the same length inside the circle. Then, join the opposite ends of the chords. That point of intersection will be the center of the circle. The circle is also part of a conic section and the foci of the conic is the center of the circle.
Then, join the opposite ends of the chords. That point of intersection will be the center of the circle. The circle is also part of a conic section and the foci of the conic is the center of the circle.
How to Find Center of Circle with Endpoints of Diameter?
The center of a circle is the midpoint of the diameter. So, by using the midpoint formula, if the endpoints of the diameter are (a, b) and (c, d), then the coordinates of the center of circle are [(a + c)/2, (b + d)/2].
How to Find Radius and Center of Circle from Equation?
If the equation of a circle is given, then we can find its radius and center by comparing it with the general form of the equation: (x – h)2 + (y – k)2 = r2. We will find the values of h, k, and r. Then, (h, k) will be the coordinates of the center of circle and r will be the radius.
Basketball court markings: standards and norms
Author of the article
Khvatkov Dmitry
Consultant in the production of rubber coatings
Basketball field marking requirements are approved by the FIBA standard. The site must be flat with a hard surface, free of bends, cracks and other obstacles. The accepted dimensions of the field are 28 m long and 16 m wide. By NBA standards, the field is slightly larger: 28.7 m (94′ ft) long and 15.3 m (50′ ft) wide.
The site must be flat with a hard surface, free of bends, cracks and other obstacles. The accepted dimensions of the field are 28 m long and 16 m wide. By NBA standards, the field is slightly larger: 28.7 m (94′ ft) long and 15.3 m (50′ ft) wide.
Areas not intended for international competitions may differ from accepted standards (for public use, in schools or universities, etc.) and usually vary from 20 to 28 m in length and from 12 to 16 m in width.
Basketball Court Marking Standards
Basketball court markings are conventionally divided into 5 components:
- Boundary lines. They are located along the perimeter of the site and set its size. The lines that run along the field are called side lines, and those that are behind the baskets are called front lines.
- Central line. Divides the court in half parallel to the front lines.
- Central zone. It is a circle and is placed in the middle of the center line, and, accordingly, in the center of the entire field.

- Three-point line. It is a semi-ellipse and is located around the shields on both sides of the field. It limits the close range.
- Free throw line. It is located in front of the boards parallel to the front line and is limited on the sides by paint lines.
The standard line width is 5 cm. All outlines and lines must be of the same color (usually white) and be clearly visible from anywhere on the court.
Common lines
Common lines are used to limit the playing area of the court. The side lines (along the field) according to FIBA standards should be 28 m long, and the front lines – 16 m. For public areas, deviations from the accepted standards are allowed. Typically, basketball courts in schools or gyms are made from 20 m long and 12 m wide.
Central lines
The center line is parallel to the front and divides the field exactly in half. According to the standards – it should extend beyond the side lines by 15 cm on both sides.
In the middle of the center line there is a circle with a diameter of 3.6 m, which limits the central zone of the field. In this zone, the ball is played at the beginning of the game.
Three-Point Line
Three-Point Lines are located around the backboards on both sides of the field and consist of two straight lines 2.9 long9 m and a semicircle. Straight lines run perpendicular to the front at a distance of 0.9 m from the side lines. Despite the fact that visually the distance from the ring to the side of the three-point line seems to be less than to its central part, the distance from the backboard to any point is 6.75 m.
Penalty lines
Penalty lines limit the nearest area at the backboard. They consist of a trapezoid and a free throw zone.
Despite the name, the “trapezium” is a rectangle (until 2009year it really was a trapezoid), which is located under the shield. Its dimensions are 5.8 meters long and 4.9 meters wide. The shield is located at a distance of 1. 575 m from the end line in the middle of the site. In front of the backboard, at a distance of 1.25 m, there is a semicircle that limits the area for picking up the ball.
575 m from the end line in the middle of the site. In front of the backboard, at a distance of 1.25 m, there is a semicircle that limits the area for picking up the ball.
At a distance of 4.225 meters from the backboard, the trapeze zone ends and the free throw zone begins. It is a semicircle with a diameter of 3.6 m (like the central circle).
Paint zone lines
These lines are serifs on both sides of the trapezoid (parallel to the sidelines). They limit the areas for players who are fighting for the ball during a free throw.
Zones on the basketball field
The basketball court is divided into zones using markings. Each zone has its own specific rules.
Center circle
The center circle is used as a separate kick-off area at the start of the game. One representative from each team stand in a circle from their side and fight for the ball in a jump, after it is dropped by the referee. All players are exclusively on their side of the field, except for one who rebounds on the opponent’s side.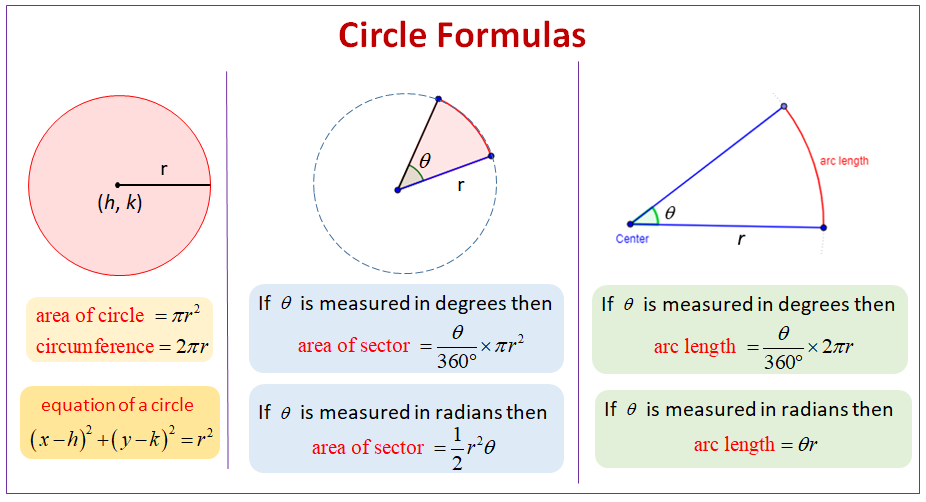
Neutral zone
The peculiarity of this zone is that as soon as the player of the attacking team with the ball crosses the center line and is on the side of the opponent, he cannot pass the ball to the player of his team who is on the other side of the field (i.e. behind center line on your side).
Three-point zone
The three-point line limits the near zone of the shot. Hitting the basket from outside the basket brings the team three points. If the throw was made inside the zone, then it brings two points.
Three-second zone
This is the zone in close proximity to the ring. It is called three-second, since the player of the attacking team cannot be in it for more than three seconds. Most balls are thrown in this zone, so when attacking, it provides maximum protection.
Free throw area
In controversial situations, a free throw is provided from this area. The player of the attacking team must score the ball without stepping over the line of the trapezoid. At the same time, the players of both teams are not in the three-second zone. They take up positions along the paint lines on the sides of the trapezoid and may not step outside the lines until the free throw shooter has shot the ball.
At the same time, the players of both teams are not in the three-second zone. They take up positions along the paint lines on the sides of the trapezoid and may not step outside the lines until the free throw shooter has shot the ball.
How to mark a basketball field?
Basketball field markings, whether it is an international competition court or an open-air amateur field, are best applied using special equipment. This will ensure the long life of the coating, the lines will not clog and will promote fair play.
You can order the marking of a basketball court in Moscow and the Moscow region from Rezkom. We will measure the premises and develop a design project for the field so that it complies with generally accepted rules and is convenient for operation. For more details, you can contact our manager by phone 8-495-64-24-111.
Ivanov V. Central circle
- pdf format
- size 8.9 MB
- added
December 26, 2010
M . : “Physical culture and sport”, 1973. – 256 p.
: “Physical culture and sport”, 1973. – 256 p.
Famous football player, forward of the Moscow “Torpedo” and the national team
team of the USSR Valentin Ivanov performed in those happy for our
football years when the team won the titles of the champion of the Olympic
games and the European Cup. Partners and comrades of Ivanov on the national team and
“Torpedo” were Yashin and Netto, Simonyan and Bobrov, Shesternev and
Metreveli, Meskhi and Monday, Muntyan and Byshovets. Ivanov is now
head of the Torpedo team. In the book, he talks about his journey to
football, about your friends, partners, rivals, and all this
material serves him to talk about the most pressing problems
modern Soviet football, which he tries to look at
simultaneously from the positions of the player and the coach.
See also
Directory
- djvu format
- size 5.52 MB
- added
August 31, 2011
M. : “Moskovskaya Pravda”, 1984. – 64 p. The book is dedicated to the championship of the Soviet Union in 1984 (second round), as well as the European Championship 1984 years in France.
: “Moskovskaya Pravda”, 1984. – 64 p. The book is dedicated to the championship of the Soviet Union in 1984 (second round), as well as the European Championship 1984 years in France.
Directory
- djvu format
- size 1.29 MB
- added
September 08, 2011
M.: “Moskovskaya Pravda”, 1959. – 97 p. The reference book is devoted to the past football championship of the Soviet Union in 1958, as well as the upcoming USSR championship 1959 years old (first round).
- doc format
- size 2.37 MB
- added
December 25, 2010
M.: “Military publishing house of the Ministry of Defense of the USSR”, 1973. – 147 p. CSKA… Central Army Sports Club. How widespread is the fame, how immense is the popularity of this club! He is well known to all athletes of our country. His sports life is closely followed by a huge mass of sports fans. CSKA has gained respect in sports circles around the world. For most fans of army sports, the concept of CSKA is associated primarily with hockey and f…
– 147 p. CSKA… Central Army Sports Club. How widespread is the fame, how immense is the popularity of this club! He is well known to all athletes of our country. His sports life is closely followed by a huge mass of sports fans. CSKA has gained respect in sports circles around the world. For most fans of army sports, the concept of CSKA is associated primarily with hockey and f…
- pdf format
- size 13.97 MB
- added
October 03, 2011
Leningrad: “Lenizdat”, 1987. – 112 p., 2nd ed., revised. and additional Honored Master of Sports L.G. Ivanov, a popular goalkeeper in the past, who defended the gates of the Leningrad Zenit for eighteen years, talks about himself, about his friends – the players of Zenit, the national teams of Leningrad and the Soviet Union, about the most memorable matches, about how the best traditions are preserved and multiplied Leningrad football. The book is intended for a wide range of readers…
The book is intended for a wide range of readers…
Directory
- pdf format
- size 13.22 MB
- added
November 21, 2011
Minsk: Publishing House of the Central Committee of the CPB, 1954. – 59 p. The directory-calendar shows the results of the national football championship of 1954 in class “A” for 1 round, and also shows the calendar of games for the second round of the USSR championship in classes “A” and “B” of season 1954 years old.
Directory
- pdf format
- size 9.42 MB
- added
August 31, 2011
M .: “Central Stadium named after V. I. Lenin”, 1991. – 62 p. Results of the penultimate 53rd championship of the USSR in 1990 (figures, statistics, results, teams, etc.). The story of the USSR Cup 1989-1990 A smooth transition to coverage of the future national championship in 1991 (as it turned out – the last one), as well as the USSR Cup (lineups, calendar of games, etc.). A lot of information about the USSR national team, a review of its performances on the international arena in 1990…
I. Lenin”, 1991. – 62 p. Results of the penultimate 53rd championship of the USSR in 1990 (figures, statistics, results, teams, etc.). The story of the USSR Cup 1989-1990 A smooth transition to coverage of the future national championship in 1991 (as it turned out – the last one), as well as the USSR Cup (lineups, calendar of games, etc.). A lot of information about the USSR national team, a review of its performances on the international arena in 1990…
Directory
- pdf format
- size 8.92 MB
- added
29December 2011
M.: “Moskovskaya Pravda”, 1975. – 96 p. The reference book is dedicated to the 1975 Soviet Union football championship (first round), the 1975 USSR Cup, as well as international competitions with the participation of Soviet teams.
Directory
- pdf format
- size 12.
 87 MB
87 MB - added
September 04, 2011
M.: “Moskovskaya Pravda”, 1981. – 96 p. The brochure is dedicated to the championship of the Soviet Union in 1981 (second round), as well as the USSR Cup and other football events in the country and the world.
Directory
- pdf format
- size 12.58 MB
- added
September 04, 2011
M.: “Moskovskaya Pravda”, 1983. – 95 p. The brochure is dedicated to the championship of the Soviet Union in 1983 (second round), as well as the USSR Cup, the Spartakiad and other football events in the country and the world.
- pdf format
- size 11.36 MB
- added
December 27, 2010
M.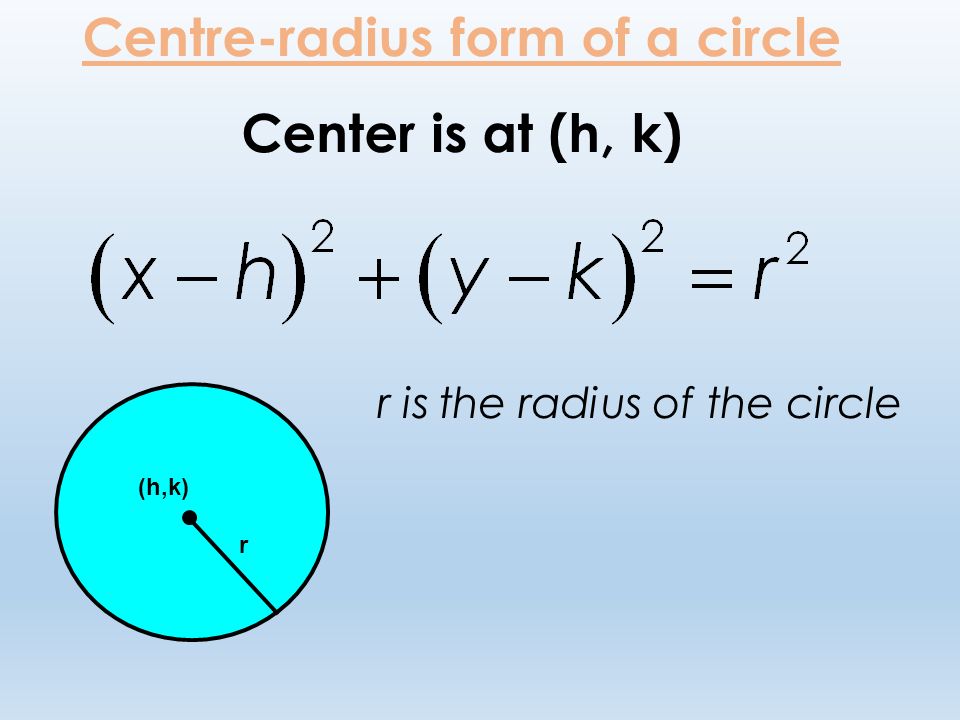


 87 MB
87 MB